Sezginin matematiği için yapay zeka

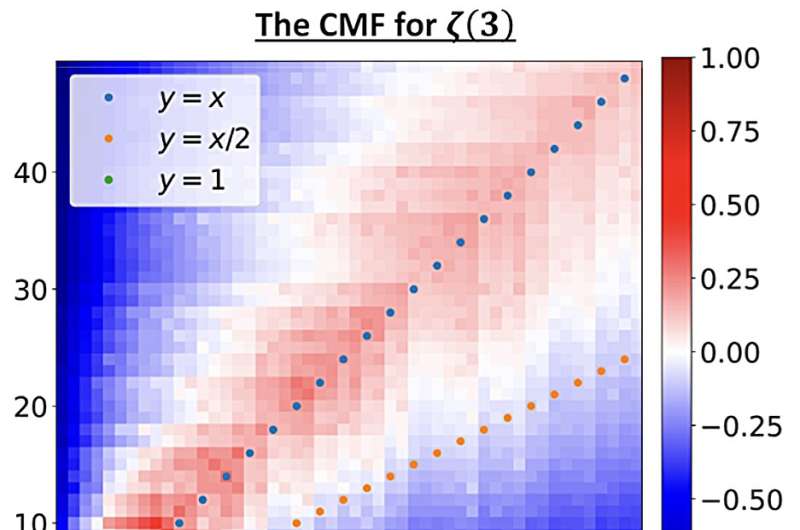
Proceedings of the National Academy of Sciences’da yayınlanan yeni bir çalışma, karmaşık matematik problemlerini çözmek için yapay zekayı (AI) kullanmaya başladı. Araştırmacılar, özellikle sayı teorisindeki karmaşık problemlerin gelişmiş hesaplama modellerin karmaşık denklemleri nasıl çözebileceğini gösterdi.

Araştırmaları, matematiksel sabitleri genelleştiren ve sayı teorisinde yeni formüller ve bağlantılar oluşturulmasına olanak tanıyan yenilikçi bir yapı olan konservatif matris alanı kavramını tanıtıyor. 

Sayılar Teorisi

Elimelech, Kaminer ve meslektaşları, bilgisayar algoritmalarının matematiksel sezgiyi otomatikleştirebileceği veya artırabileceği olasılığını araştırıyorlardı. Bu, onları matematiksel araştırmaları hızlandırmak için algoritmalar geliştirmeyi amaçlayan yeni bir işbirliği çabası olan Ramanujan Makinesi araştırma grubunu kurmaya teşvik etti.

“Sayılar teorisi gibi alanlarda, ilerlemeler genellikle yaratıcılığa veya insan sezgisine atfedilir.”diyor makalenin yazarları Rotem Elimelech ve Ido Kaminer ve devam ediyorlar: “Bu alanlarda, sorular yüzlerce yıl boyunca çözümsüz kalabilir ve bir cevap bulmak doğru formülü keşfetmek kadar basit olsa da bunu yapmanın net bir yolu yoktur.”

Konservatif matris alanı

‘Konservatif matris alanı’ olarak tanımladıkları alan, konservatif vektör alanına benzer olsa da bu alanda çizgi integrallerini kullanmak yerine matris çarpımları yoluyla hesaplama yapılıyor. Diğer bir deyişle bu araştırma, yüklü bir parçacığın yarattığı elektrik alanında potansiyeldeki değişimi çizgi integrallerini kullanarak hesaplanan konservatif vektör alanı yerine, iki nokta arasındaki potansiyel değişimi matris çarpımıyla yapmayı içeriyor.

Konservatif matris alanın önemli bir avantajı, her matematiksel sabitin formüllerini genelleştirebilmesi ve aynı türden sonsuz sayıda yeni formül üretebilmesidir.

Karmaşık problemleri çözmek için birlikte çalışan birden fazla birbirine bağlı düğümün kullanımını gerektiren büyük ölçekli dağıtılmış bilgi işlem kullanılıyor. Bu yaklaşım, temel sabitler için yeni rasyonel diziler, diğer bir deyişle formüller, keşfedilmesine olanak sağladı.

Matematik meraklılarına davet

Ekibin bilgisayar bilimi, elektrik mühendisliği, matematik ve fiziği birleştiren uygulamalı yaklaşımı, Katalan sabitinin irrasyonelliği ve Riemann zeta fonksiyonu gibi uzun süredir devam eden matematiksel gizemleri ele almayı amaçlıyor. Vizyonları, bu yapay zeka odaklı deneysel matematik yaklaşımını daha geniş bir sorun yelpazesine genişletmeyi ve potansiyel olarak matematik ve fizikteki araştırmaları devrim niteliğinde değiştirmeyi içeriyor.

Elimelech ve Kaminer, “Algoritmalarımız tarafından oluşturulan kanıtlanmamış hipotezleri düzenli olarak yayınlıyoruz ve diğer matematik meraklılarını bu hipotezleri kanıtlamaya davet ediyoruz ve doğrulandığında proje web sitemizde yayınlıyoruz.” dediler.

Kaynak: PNAS